Science
표준편차 구하는 방법
Jay1Seo
2024. 2. 18. 05:51
반응형
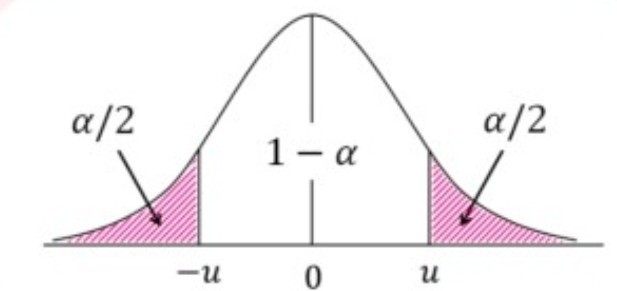
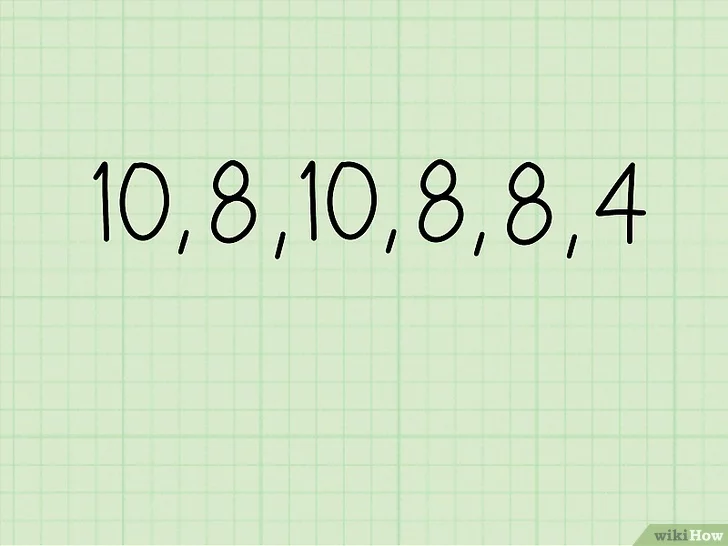
- 1
- 주어진 자료 보기. 통계적인 계산을 할 때는 항상 주어진 자료를 먼저 자세히 살펴보는 습관을 지녀야 한다. 심지어 평균이나 중간값 같은 단순한 수치를 구한다 해도 말이다.[3]
- 일단 주어진 자료에 얼마나 많은 숫자가 있는지 살펴본다.
- 숫자가 작은 수부터 큰 수까지 널리 분포되어 있는가? 아니면 크기가 비슷한 숫자끼리 모여 있는가? 주어진 자료의 숫자가 아주 약간의 차이밖에 안 나는가?
- 주어진 자료가 나타내는 것이 무엇인지 이해해야 한다. 자료의 숫자들은 성적일 수도 있고, 심박수일 수도 있으며, 키나 몸무게일 수도 있다.
- 예를 들어 우리에게 주어진 시험 성적 자료가 10, 8, 10, 8, 8, 4로 나타날 수 있을 것이다.
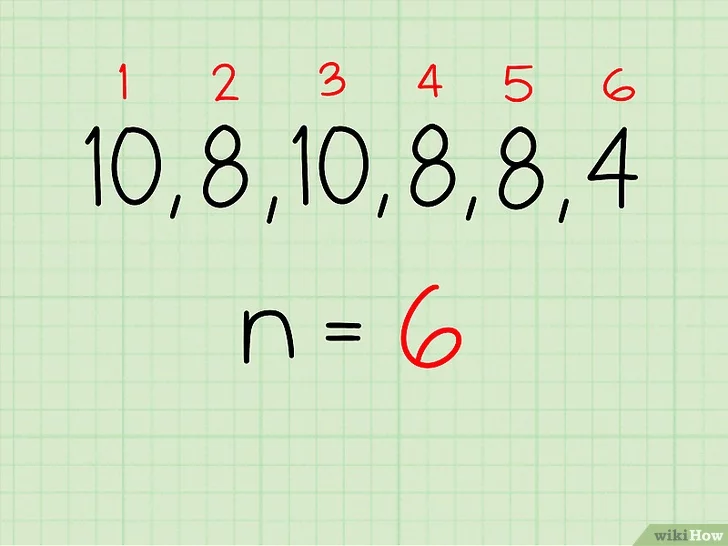
- 2
- 자료 모으기. 자료에 속한 모든 숫자를 동원해 먼저 평균을 계산하도록 한다.[4]
- 평균값은 말그대로 평균을 구하면 된다.
- 평균을 구하려면 먼저 주어진 자료(n)의 모든 숫자를 더한 뒤에 더한 숫자의 개수로 나누면 된다.
- 아까 주어진 성적 자료의 평균을 구해보면 다음과 같다. 먼저 자료는 (10, 8, 10, 8, 8, 4)처럼 집합으로 나타내고 숫자가 6개 있으므로 n = 6이 된다.
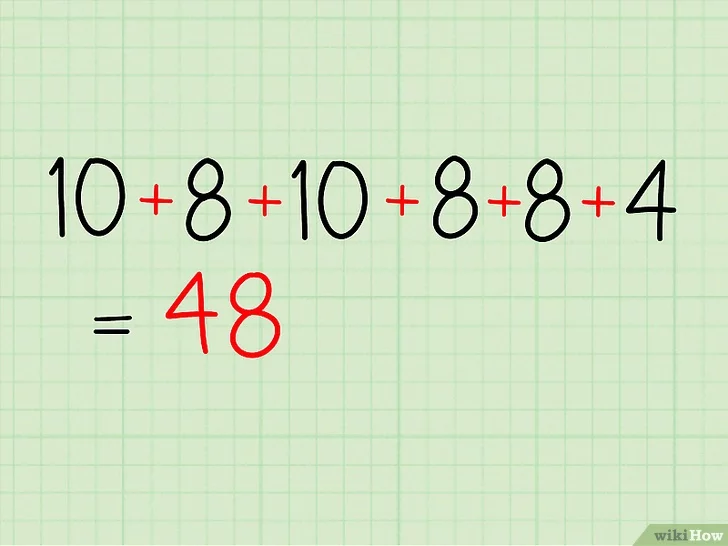
- 3
- 자료의 숫자를 모두 더하기. 평균을 구하기 위한 첫 번째 단계이다.[5]
- 아까의 예시를 계속 이어서 풀어보겠다. 시험 성적 자료는 다음과 같았다: 10, 8, 10, 8, 8, 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. 이처럼 먼저 자료의 수를 다 더해준다.
- 다시 한 번 덧셈을 해 검산을 한다.
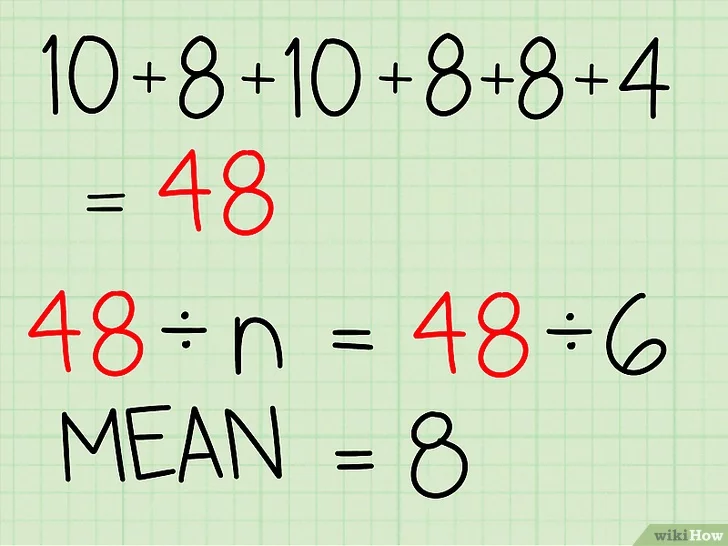
- 4
- 이제 전 단계에서 구한 n으로 총합 나누기. 그러면 현재 주어진 자료의 평균값이 나오게 된다.[6]
- 아까 계산한 시험 성적 자료 (10, 8, 10, 8, 8, 4)에는 숫자가 여섯 개 있었으므로 n = 6으로 쓸 수 있다.
- 시험 성적을 다 합치면 48이 되므로 이제 이를 n으로 나눠 평균을 구할 수 있다.
- 48 / 6 = 8
- 즉 시험 성적의 평균은 8점이다.
파트
2
분산 구하기
- 1
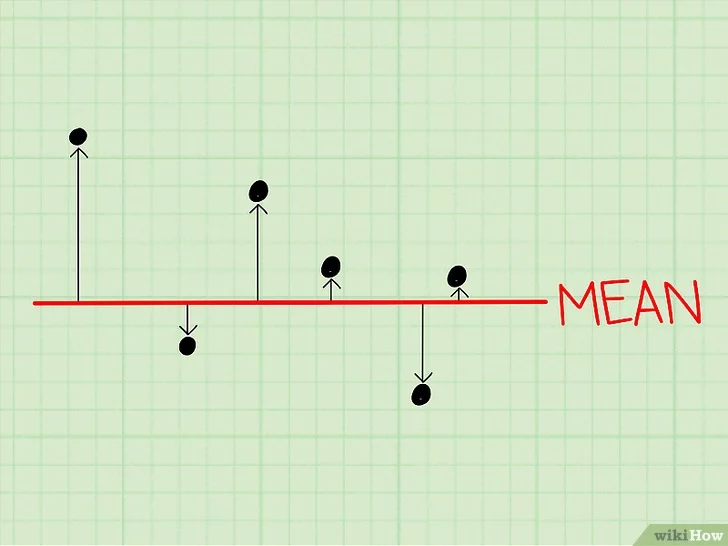
- 분산 구하기. 분산이란 주어진 자료의 숫자가 평균을 기준으로 어떻게 흩어져 있는지 나타내는 지표이다.[7]
- 분산은 전체적으로 숫자가 어떻게 흩어져 있는지 설명해준다.
- 분산이 작으면 숫자가 평균값 근처에 모여있다는 말과 같다.
- 분산이 크면 말 그대로 숫자가 평균값과 멀리 떨어져 있다는 뜻이다.
- 분산은 두 자료의 흩어진 정도를 비교할 때 자주 사용된다.
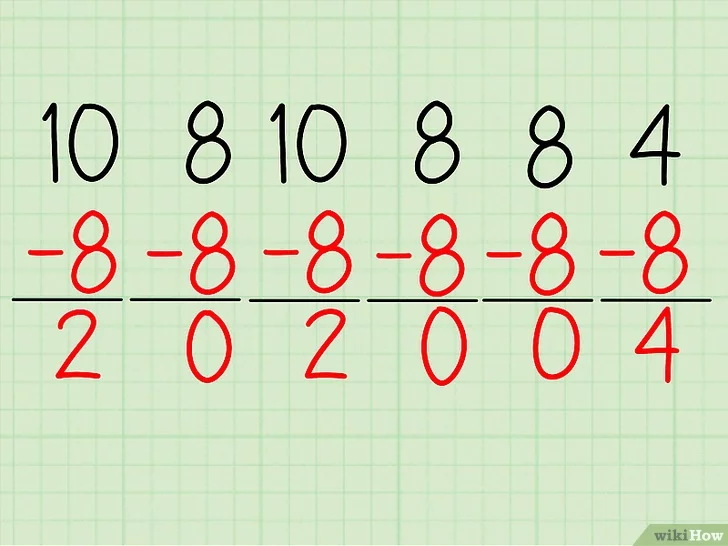
- 2
- 자료의 수에서 평균값 빼기. 이 과정을 통해 자료 속의 각 숫자가 평균값에서 얼마나 멀리 떨어져 있는지를 알 수 있다.[8]
- 예를 들어 아까 시험 성적을 다시 보도록 하자. (10, 8, 10, 8, 8, 4)의 평균으로 8을 구했었다.
- 이제 각 숫자에서 평균을 빼면 다음처럼 될 것이다. 10 - 8 = 2, 8 - 8 = 0, 10 - 8 = 2, 8 - 8 = 0, 8 - 8 = 0, 4 - 8 = -4.
- 이 과정을 다시 한 번 반복해 검산하도록 한다. 한 번 실수하면 이후의 과정이 다 틀려질 수 있으므로 꼭 검산을 하도록 한다.

- 3
- 평균값을 빼고 나온 값을 제곱하기. 자료 속의 숫자에서 평균을 뺀 값을 각각 따로 제곱해 놓는다.[9]
- 아까 시험 성적 자료(10, 8, 10, 8, 8, 4) 에서 평균값 8을 빼고 남은 숫자는 2, 0, 2, 0, 0, -4 였다.
- 이제 각 숫자를 제곱하도록 한다. 그러면 22, 02, 22, 02, 02, (-4)2 = 4, 0, 4, 0, 0, 16로 정리된다.
- 다음 단계로 넘어가기 전에 빠르게 검산을 하도록 한다.
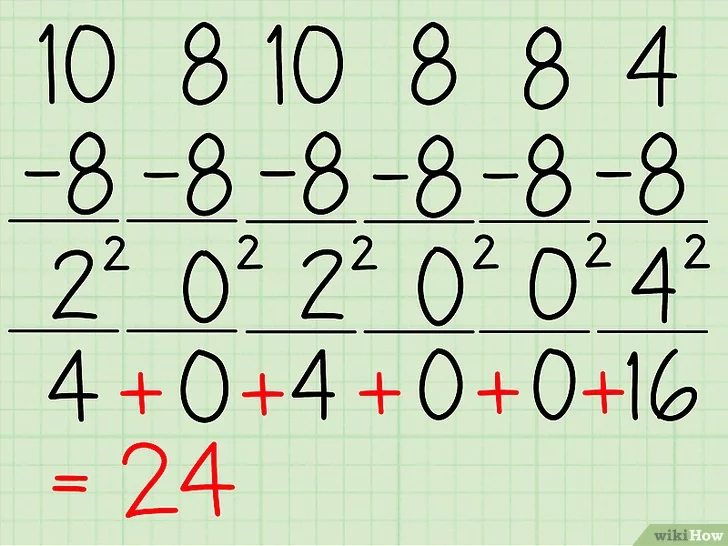
- 4
- 모든 값을 더하기. 이 과정을 제곱합이라고 부른다.[10]
- 다시 시험 성적 자료를 놓고 보면 제곱한 값은 4, 0, 4, 0, 0, 16가 나왔었다.
- 다시 설명하자면 위 값은 각 성적에서 평균값 8을 빼고 각각 제곱한 것이다. (10-8)^2 + (8-8)^2 + (10-8)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 이제 제곱한 값을 다 더해보자. 4 + 0 + 4 + 0 + 0 + 16 = 24.
- 제곱의 합은 24이다.
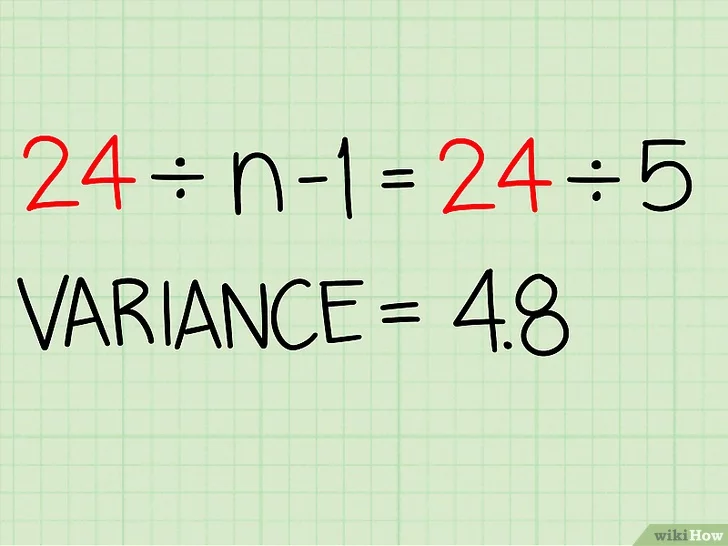
- 5
- 제곱의 합을 (n-1)로 나누기. 아까 위에서 썼지만, n은 처음 주어진 자료에 속한 숫자의 개수이다. 이 과정을 거치면 분산이 나오며, 여기서 n-1로 나누는 이유는 표본 분산과 모분산을 분리하기 위해서이다.[11]
- 시험 성적을 놓고 다시 보면 (10, 8, 10, 8, 8, 4)로 6개의 숫자가 있었다. 따라서 n = 6이다.
- n - 1 = 5.
- 제곱의 합이 24가 나왔다는 점을 참고하자.
- 24 / 5 = 4.8
- 따라서 시험 성적의 분산은 4.8가 된다.
파트
3
표준 편차 구하기

- 1
- 분산 알기. 표준 편차를 구하기 위해서는 분산이 필요하다는 점을 먼저 알도록 하자.[12]
- 분산은 주어진 자료의 숫자가 평균값을 기준으로 어떻게 분포되어 있는지 나타내는 지표다.
- 표준 편차도 분산과 마찬가지로 자료 내의 숫자가 어떻게 분포되어 있는지를 나타낸다.
- 시험 성적 예시를 다시 보자. 아까 위에서 구한 분산은 4.8이었다.

- 2
- 분산의 제곱근 구하기. 분산 값에 루트를 씌워 제곱근을 구하면 표준 편차가 나온다.[13]
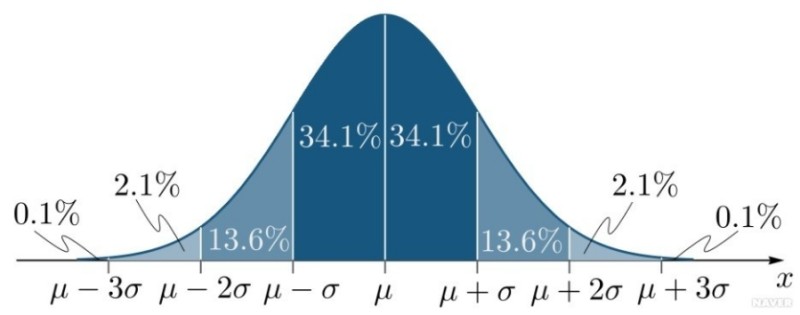
- 일반적으로 어떤 자료의 데이터 중 68%는 평균값을 기준으로 표준 편차 값을 더하거나 뺀 값의 범위를 벗어나지 않는다.
- 아까 시험 성적의 분산은 4.8이었다.
- 루트를 씌우면 다음과 같이 표준 편차가 나온다. √4.8 = 2.19. 우리가 구하고자 한 표준 편차의 값이 2.19가 됨을 알 수 있다.
- 우리 시험 성적 자료 (10, 8, 10, 8, 8, 4)를 보면 평균값 (8)에서 표준 편차 (2.19)를 더하고 뺀 값의 범위 내에 6개 중 5개, 즉 83%의 수가 속해 있는 것을 확인할 수 있다.

- 3
- 평균, 분산, 표준 편차를 다시 구해 검산하기. 이 글을 다시 쭉 따라가며 모든 수치가 맞게 계산되었는지 확인한다.[14]
- 표준 편차를 구할 때 계산기를 썼던 손으로 풀었던 모든 과정을 종이에 적어가며 푸는 것이 중요하다.
- 두 번째 구했을 때 다른 값이 나왔다면 과정을 차근차근 훑어보도록 한다.
- 어디가 틀렸는지 찾기 힘들다면 마지막으로 다시 한 번 문제를 풀어본다.
펌글 :
2022. 11. 30. 17:42
반응형